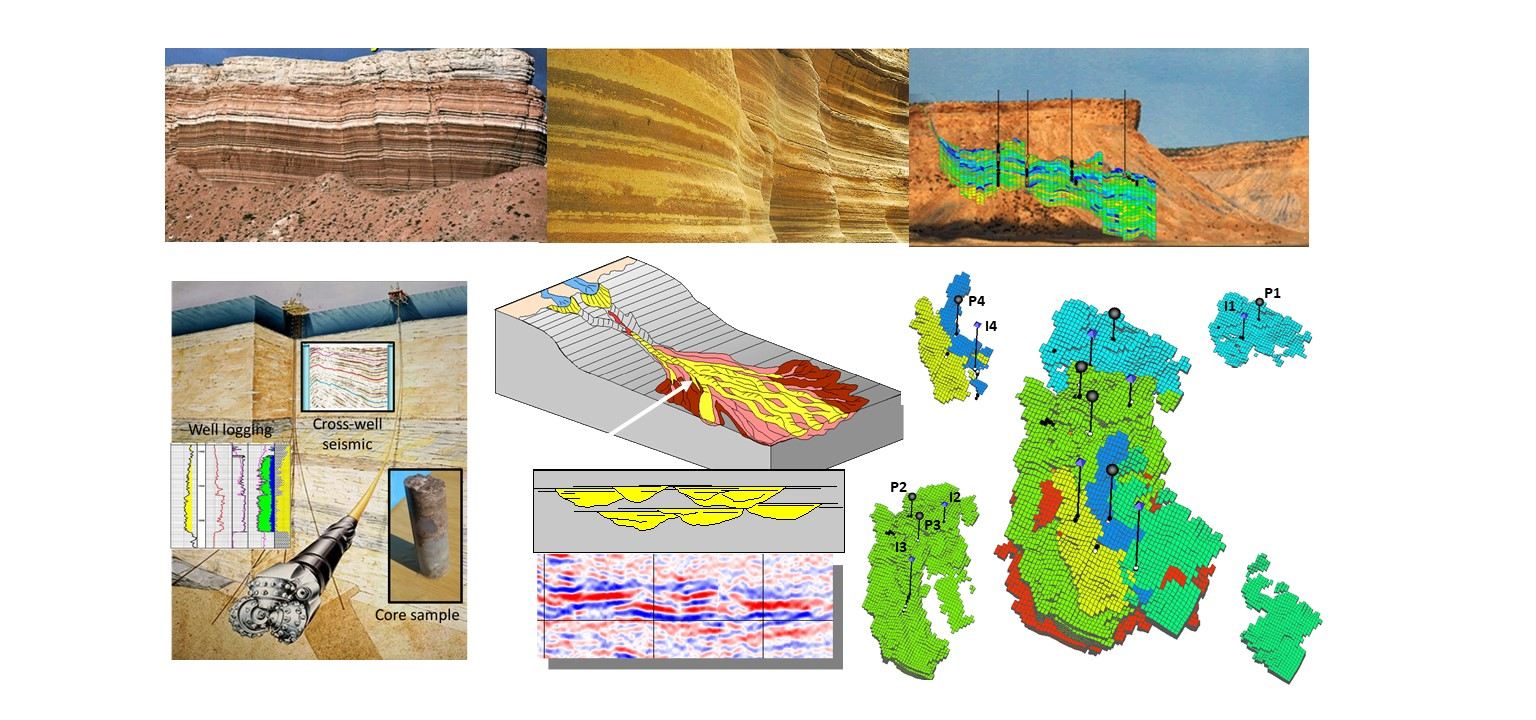
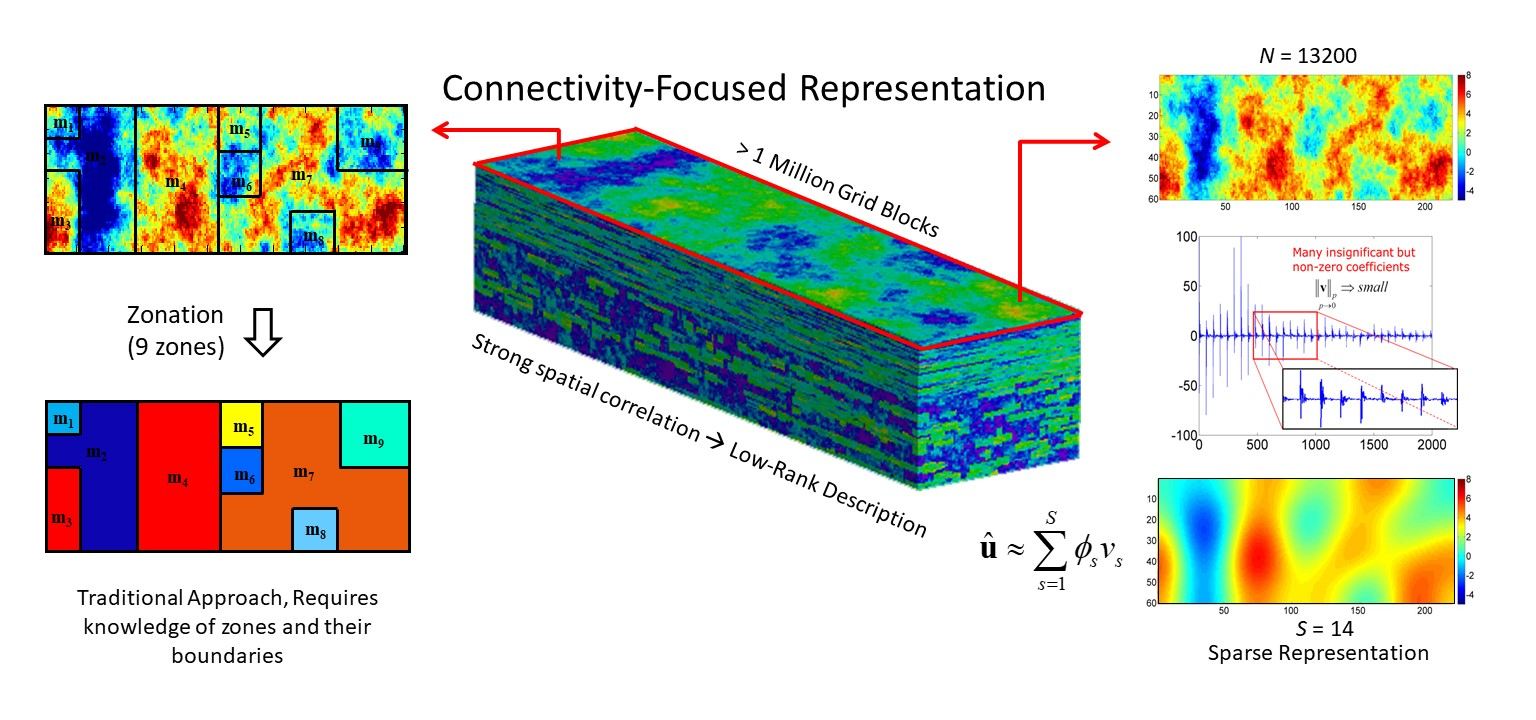
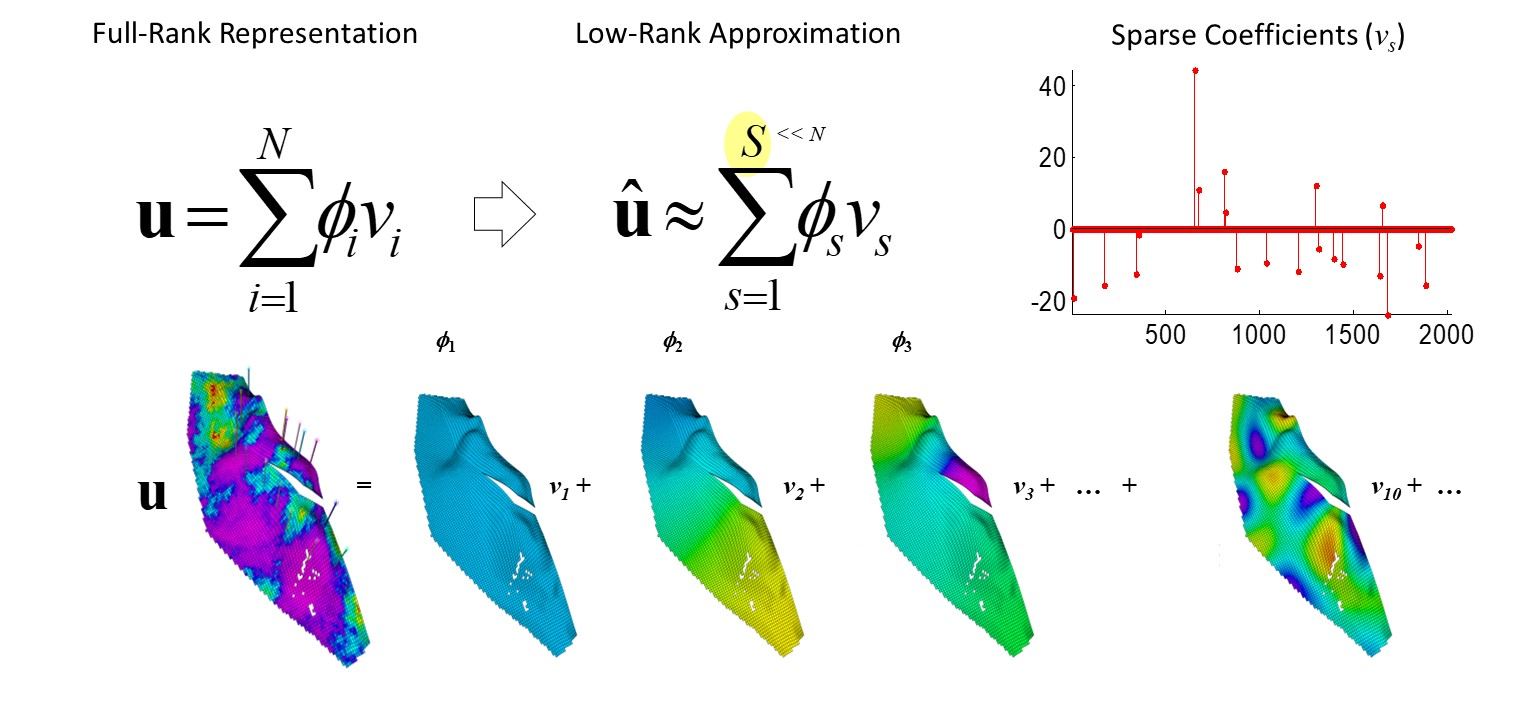
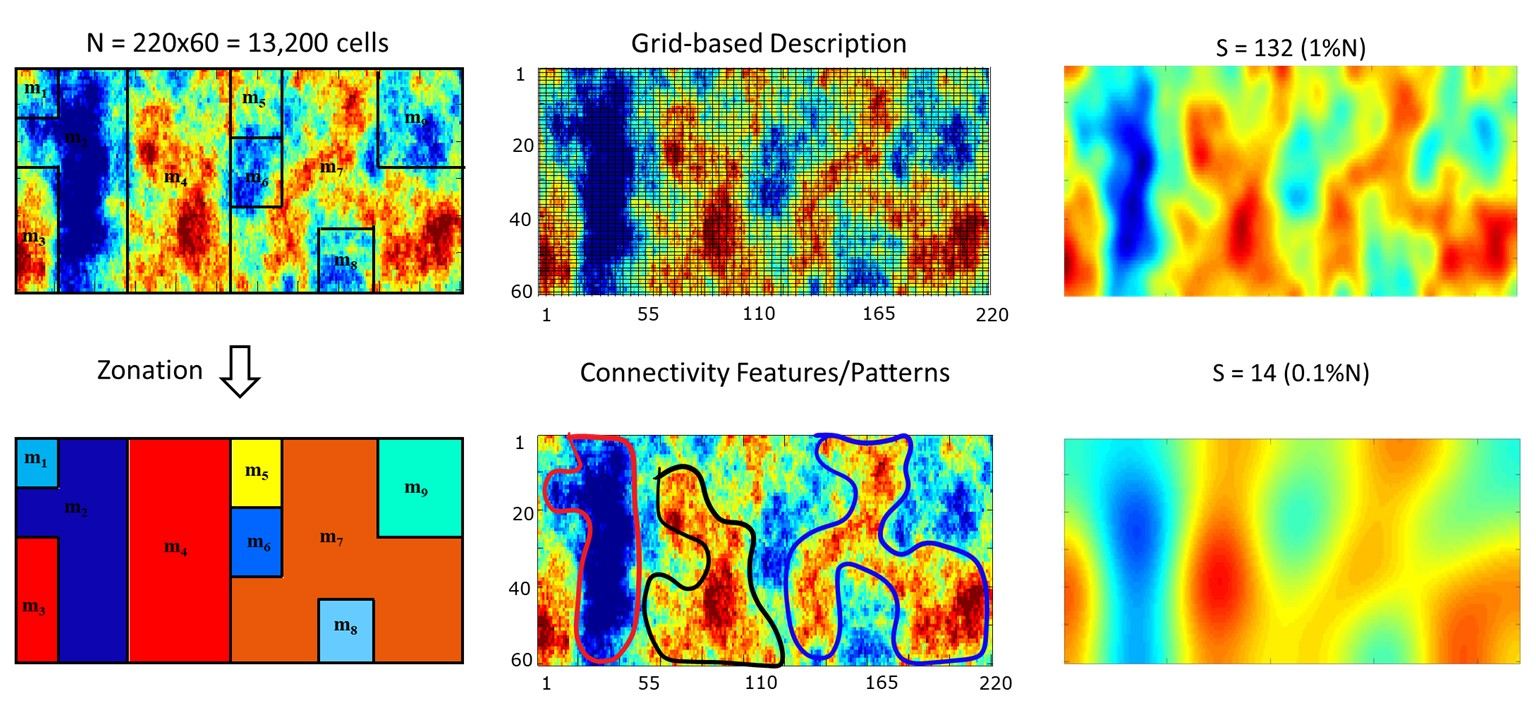
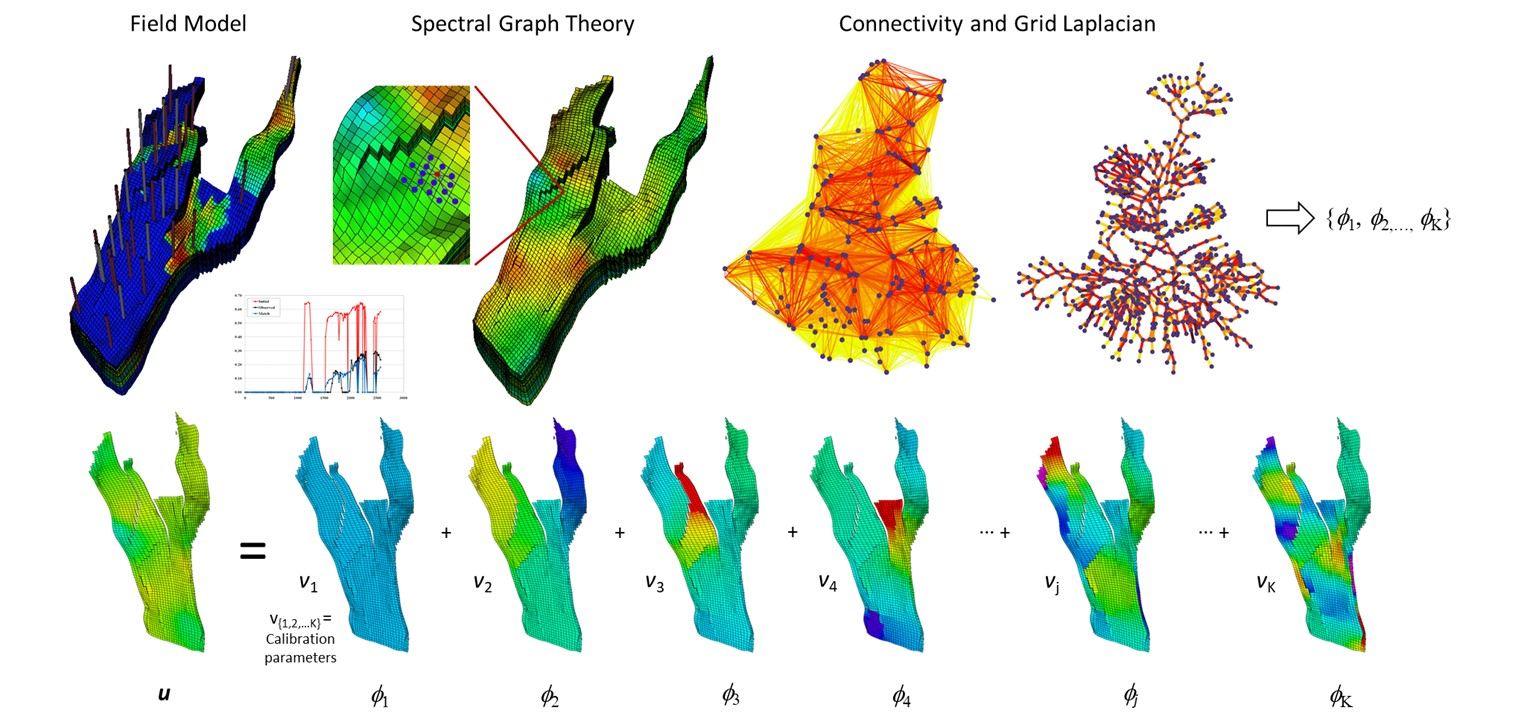
Accurate description of subsurface flow and transport properties and their spatial connectivity is critical for predicting and optimizing the development of susburface energy resources. Geologic uncertainty, the complexity of multi-scale spatial heterogeneity, as well as insufficient constraining data complicate the description and characterization of subsurface physical properties. A common practice to reduce uncertainty and to improve the accuracy and reliability of flow predictions is to use dynamic response data from scattered locations to constrain (calibrate) high-resolution subsurface flow models. However, dynamic data from limited locations do not provide sufficient content to resolve high-resolution flow models. This discrepancy calls for effective descriptions of subsurface models that can be resolved from dynamic response data. In our research, we take a feature-based description approach to represent and estimate the large-scale spatial connectivity patterns in subsurface flow properties. Geologic formations consist of layers of rock deposits with similar properties across their horizontal extent; hence, they tend to exhibit strong spatial continuity and correlation. This prevalent geologic continuity enables parsimonious representations of the related properties in a properly designed transform domain. We develop various low-rank representation methods for effective subsurface description and inverse modeling applications.
Our research in this area is inspired by signal/image processing, machine learning, and approximation theory. In our recent research, we have developed sparse representation approaches that facilitate model recovery and calibration via sparse reconstruction algorithms, including learned sparse geologic dictionaries, variational autoencoder (VAE), and generative adversarial network (GAN). Our specific research contribution in this area is developing customized low-rank representation techniques for subsurface flow inverse modeling. Of particular interest are reduced representations that can effectively describe complex (nonlinear and non-Gaussian) high-dimensional models, and robust approaches that can represent diverse spatial patterns from multiple (uncertain) geologic scenarios, to facilitate dynamic monitoring and performance data integration.