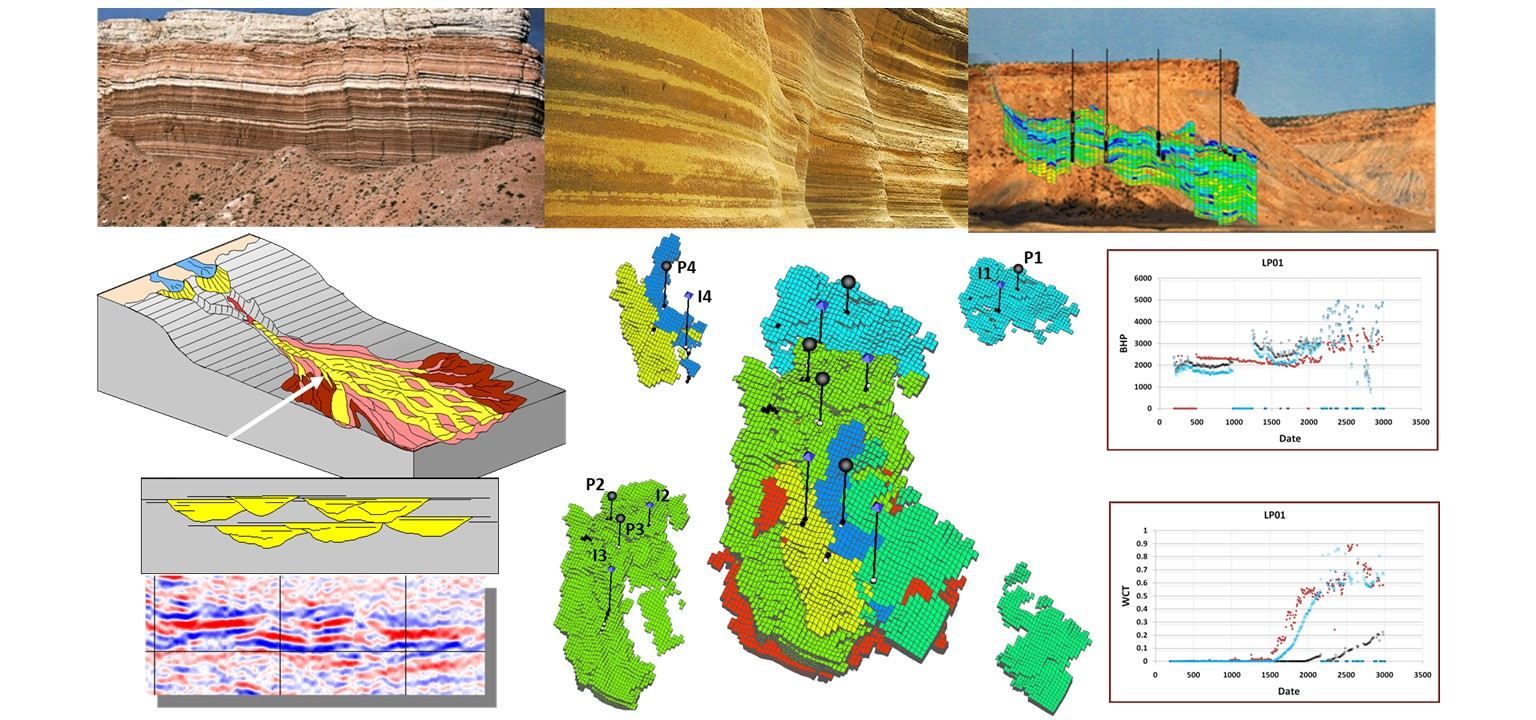
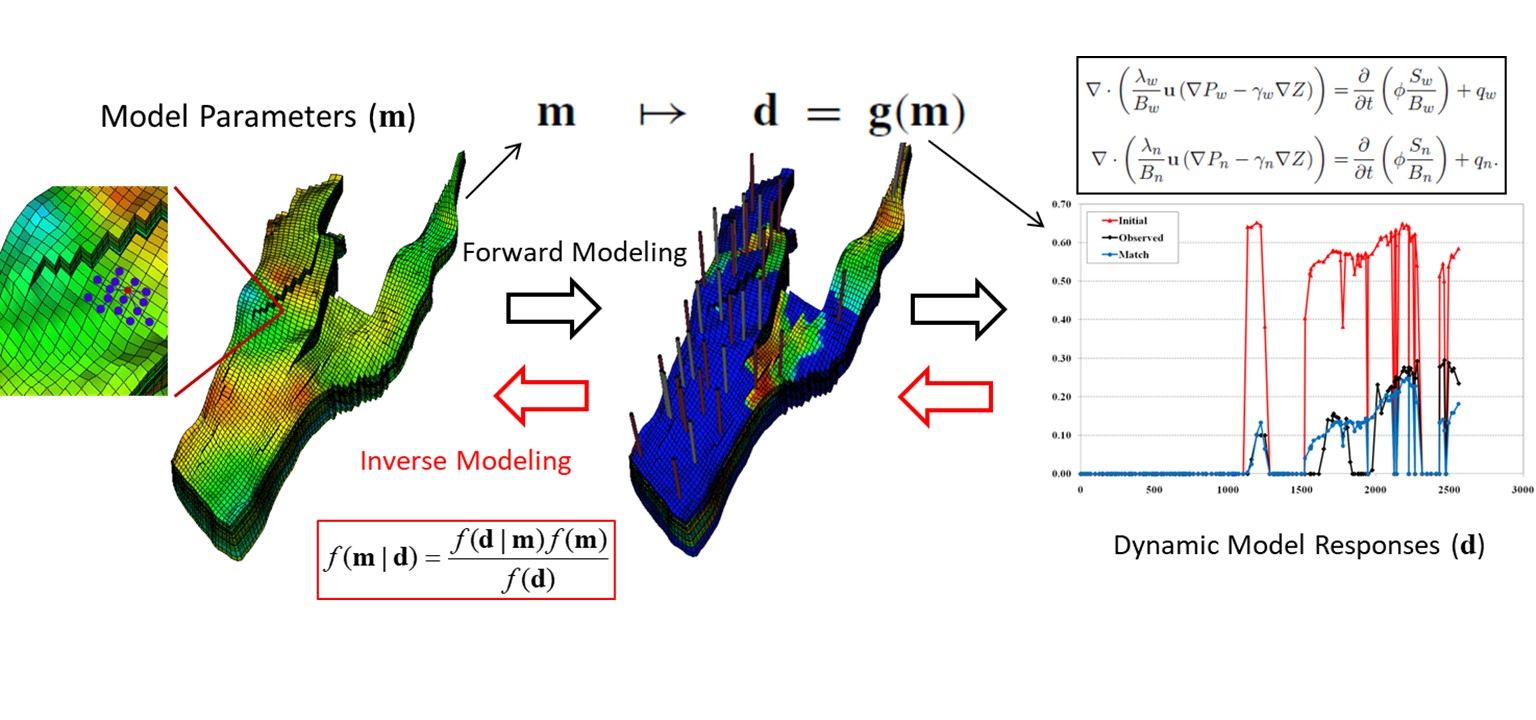
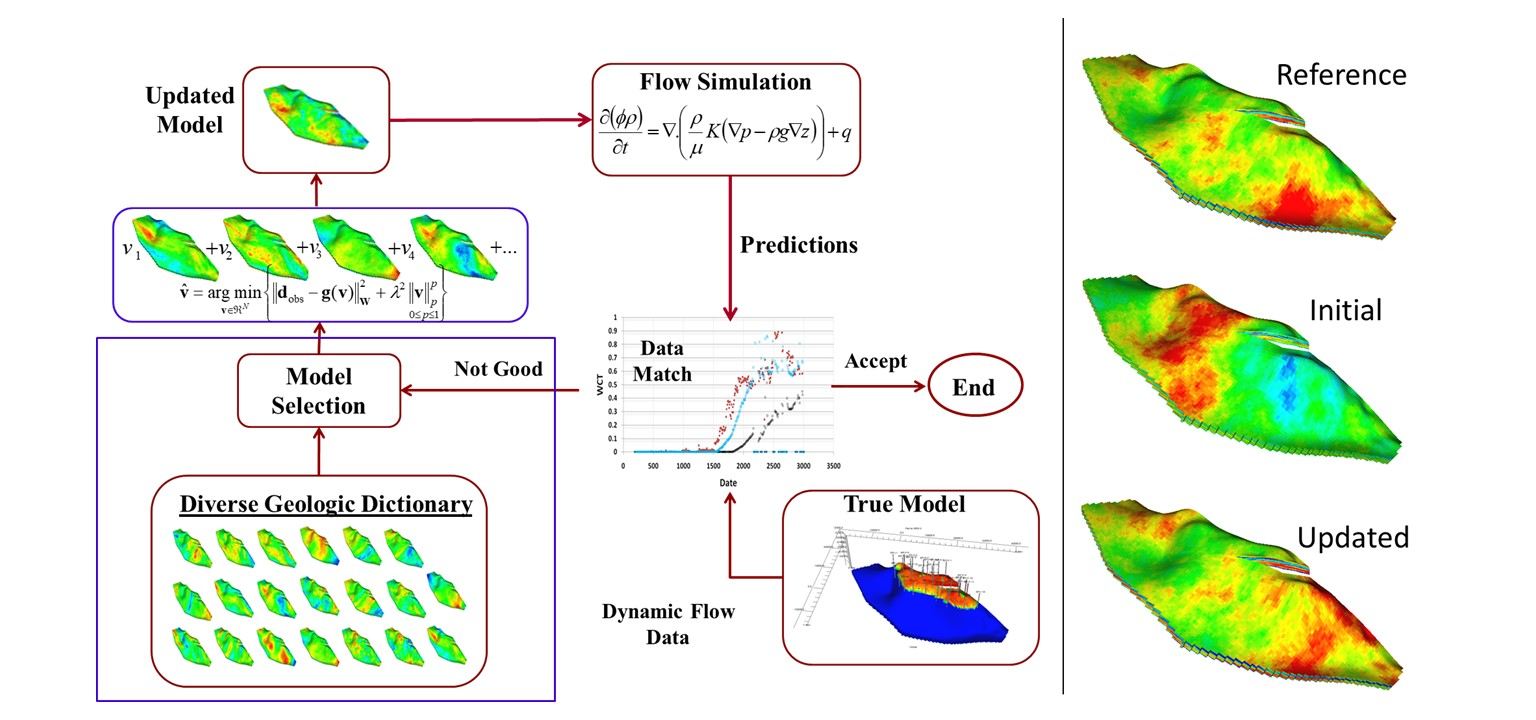
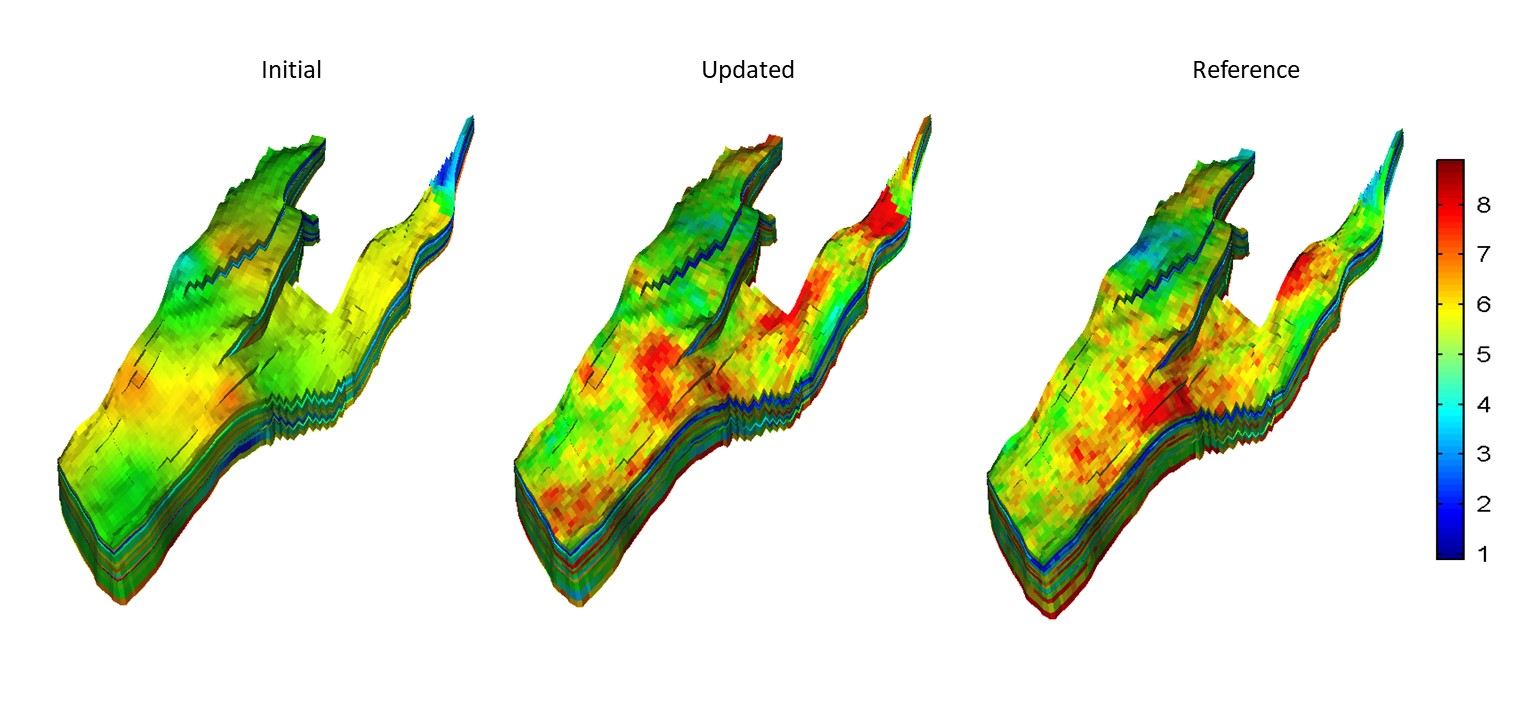
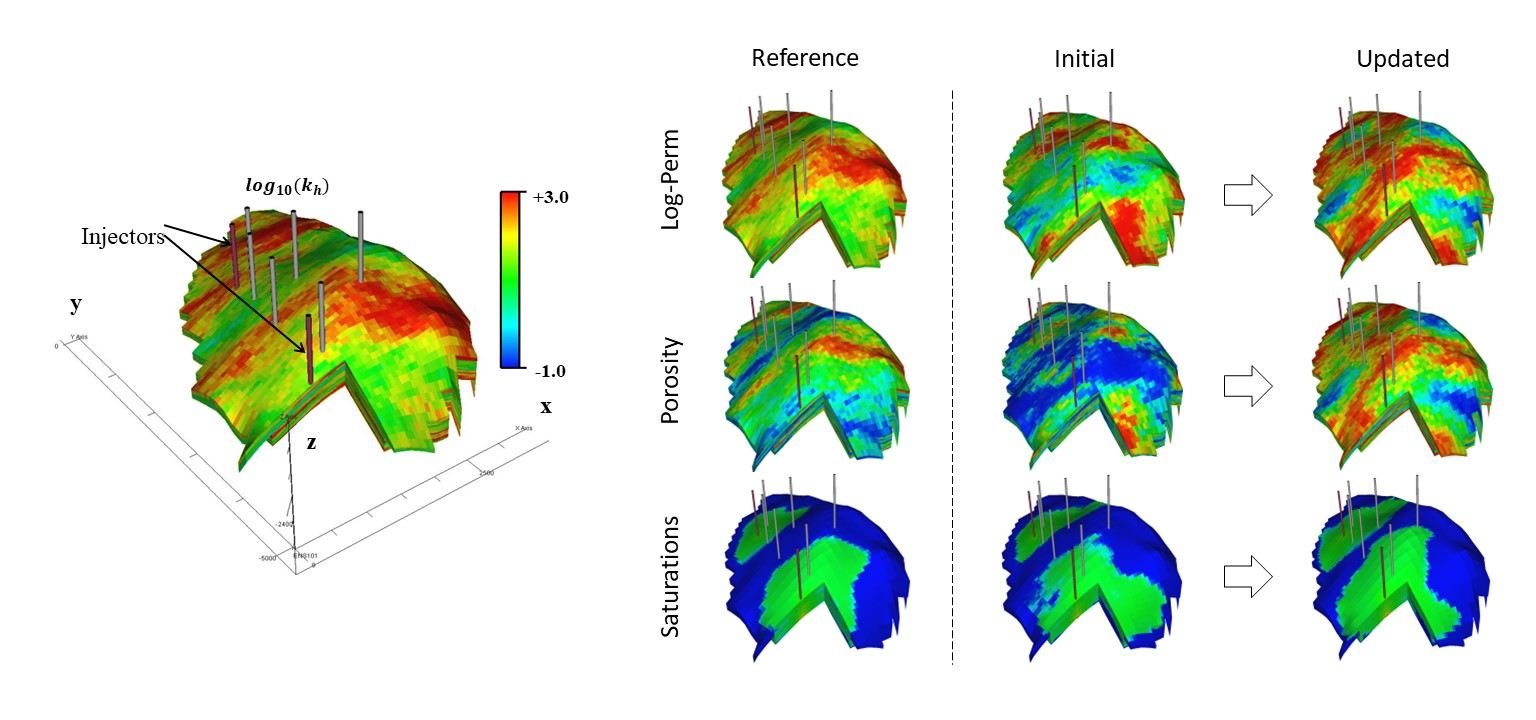
Integration of dynamic response data into subsurface flow models is commonly performed by formulating and solving an inverse problem. For heterogeneous subsurface flow models, the number of unknowns to be estimated is typically overwhelmingly greater than the available data, giving rise to an underdetermined inverse problem for which unique solutions cannot be found. Regularization and low-rankr parameterization are two common approaches that incorporate additional information (prior knowledge) to further constrain the solution of underdetermined inverse problems. To account for and quantify the uncertainties in the prior knowledge, the observed data, the nonlinear mapping from parameter space to data space, and the resulting solutions, probabilistic formulations of the inverse problem can be adopted. We develop inverse modeling frameworks for subsurface flow model calibration and uncertainty quantification applications. The main emphasis of our inversion formulations is on identifying the salient information (e.g., spatial connectivity) in important subsurface properties that dominate the flow pattern. As such, we capitalize on feature/pattern-based estimation and imaging methods to better understand and characterize the key information that dominate the flow patterns in the subsurface environments.
An important area of investigation in our lab is solving inverse problem under (global) uncertainty in the prior knowledge. In subsurface modeling, prior knowledge is derived from incomplete data using subjective interpretation and interpolation assumptions. Geologic uncertainty is one of the main challenges in developing subsurface flow models, simply because of the lack of convenient access to sufficiently sample these formations. While geologic information/expertise can provide important prior knowledge for constraining the flow and transport models, it inherently entails significant uncertainty not just about the exact location and extent of the existing geologic connectivity features but, more importantly, about the type of existing geologic features and their spatial patterns and connectivity (that is, the geologic scenario). In the conventional inverse modeling approaches, the geologic scenario is typically assumed as known and is used to constrain the solution of the inverse problem. This approach not only is prone to introducing significant bias, but it also eliminates the opportunity for the geologist to use flow data to resolve/reduce the uncertainty in geologic modeling.
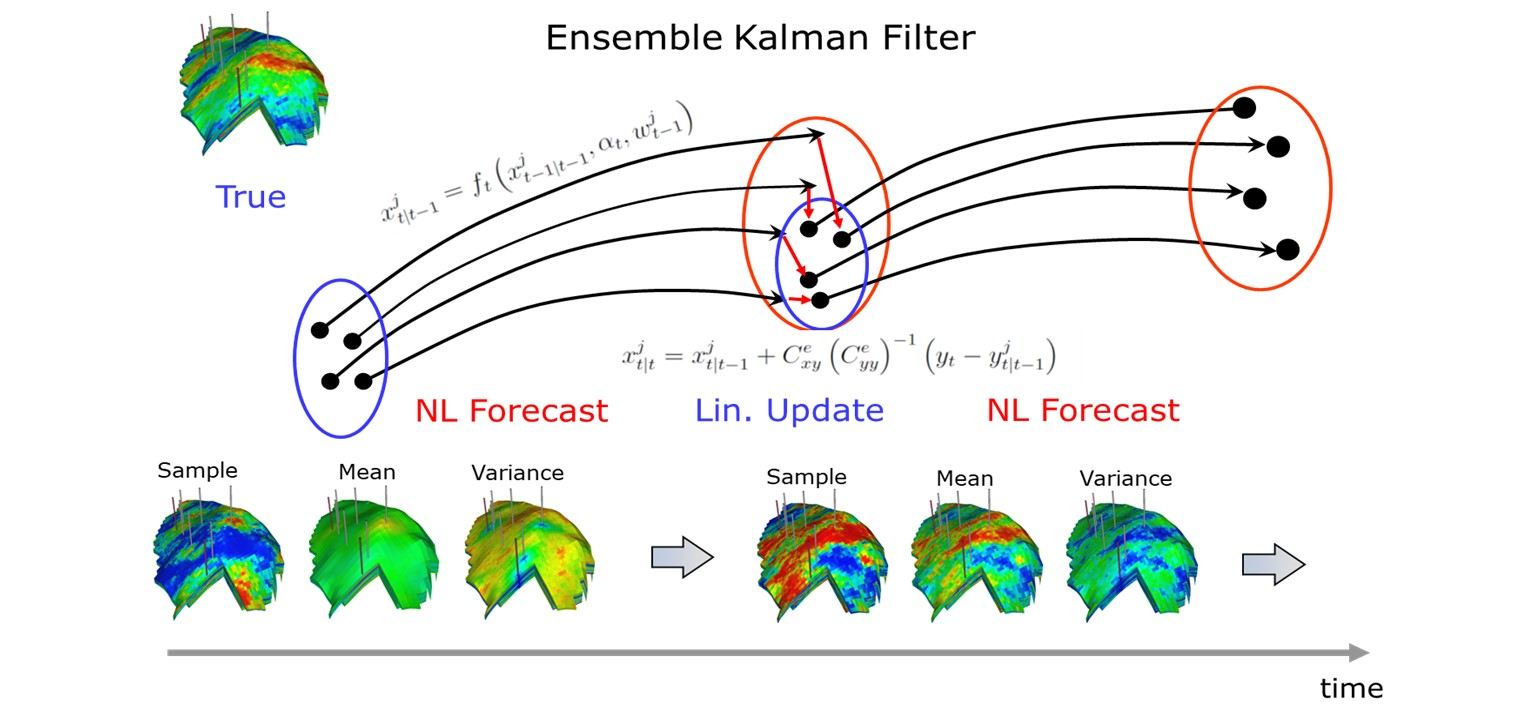
We develop inverse modeling formulations that take advantage of available prior geologic knowledge and, at the same time, account for the uncertainty in the geologic scenario. By considering the uncertainty in the conceptual geologic model, our methods make it possible to utilize dynamic flow response data to assist geologists in reducing the uncertainty in their models. This step is critical before using the prior knowledge for model calibration as it helps to eliminate scenarios that are not supported by the flow data. We also investigate and develop novel ensemble-based techniques for practical implementation of probabilistic model calibration and uncertainty quantification. Another research area of great importance in subsurface energy systems (e.g., geothermal reservoirs and geologic CO2 storage) is joint inverse modeling methods for multi-physics problems, involving flow, transport, deformation, as well as thermal effects and chemical reactions. While progress has been made in developing coupled flow simulation for predicting the behavior of these systems, research is needed to develop joint inverse modeling and uncertainty quantification frameworks for multi-physics systems.
Examples of our recent and current research projects in these areas include:
- Deep learning for low-rank parameterization and inverse modeling
- Pattern-based dynamic data conditioning for complex geosystems
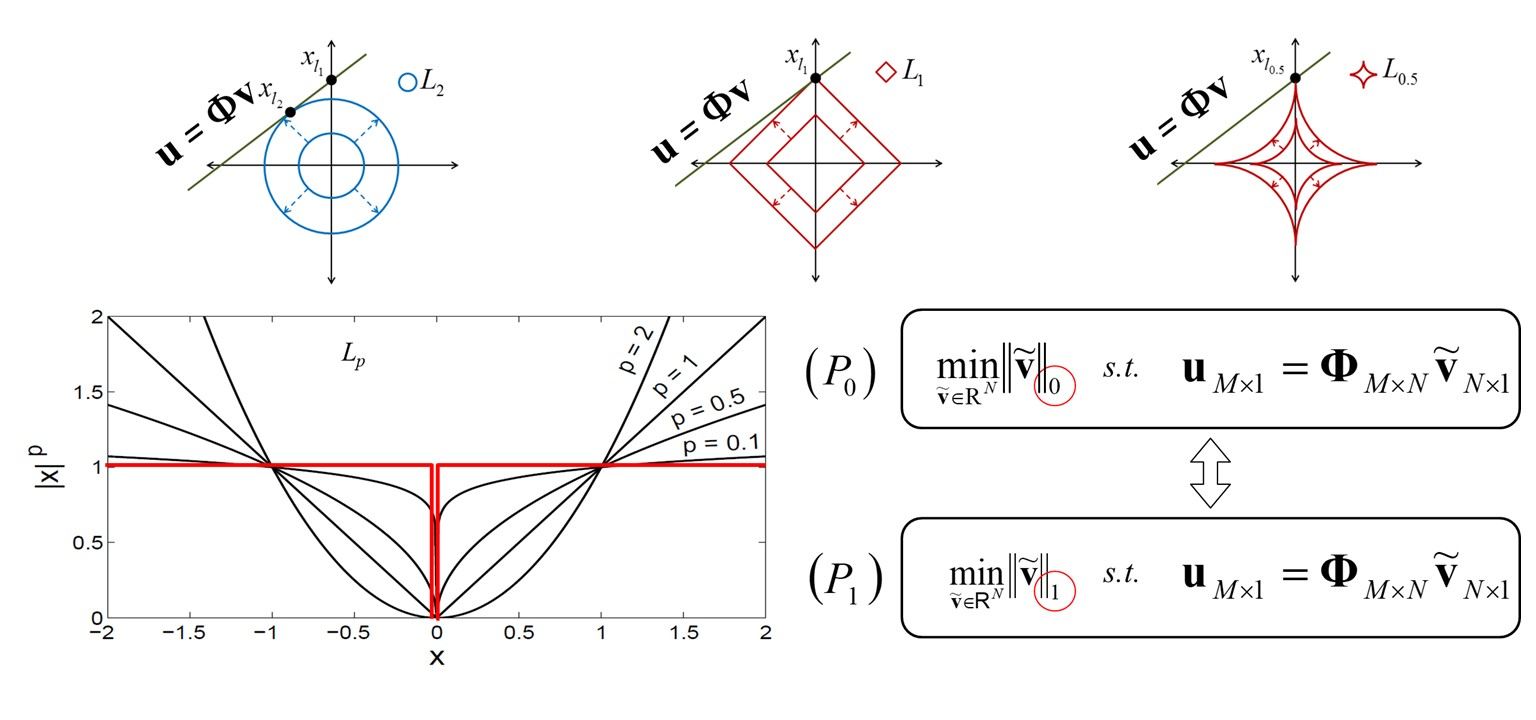
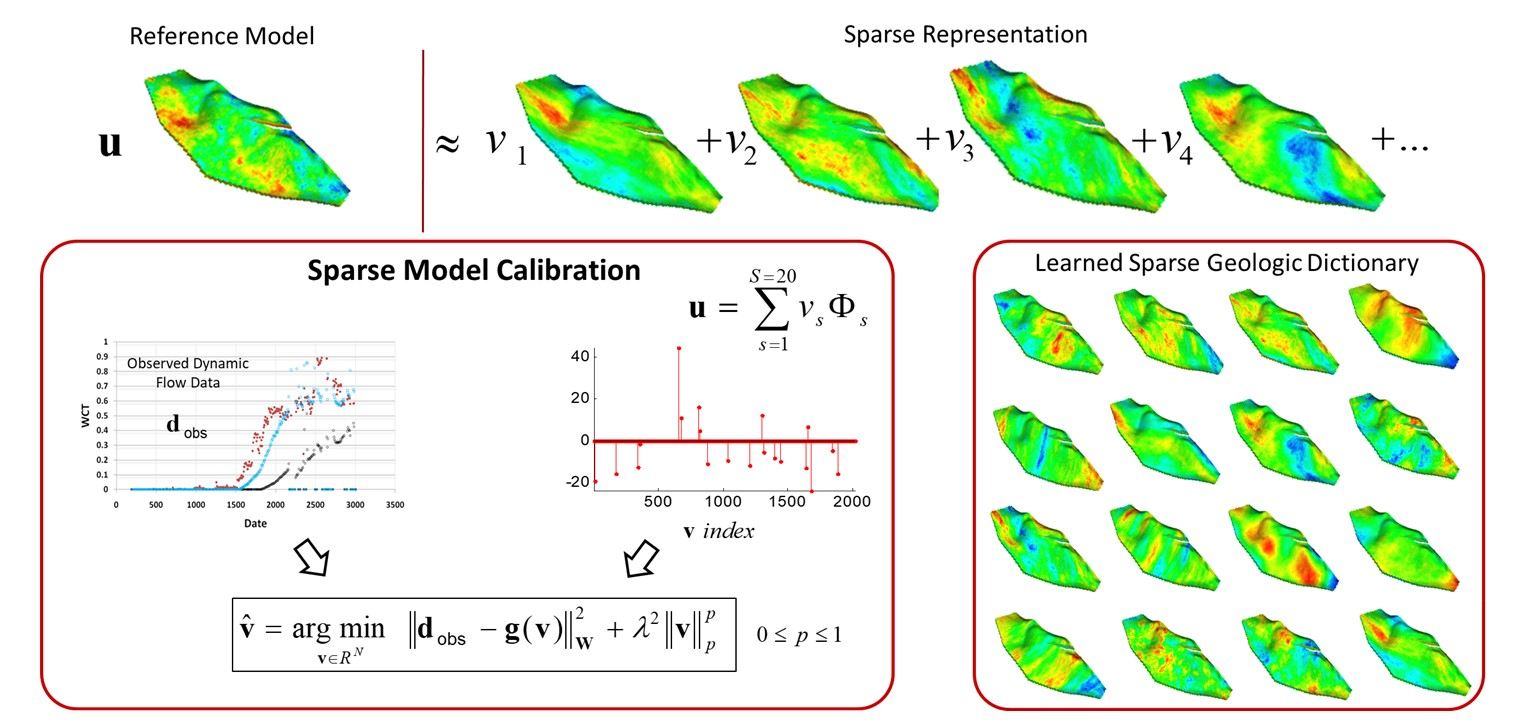
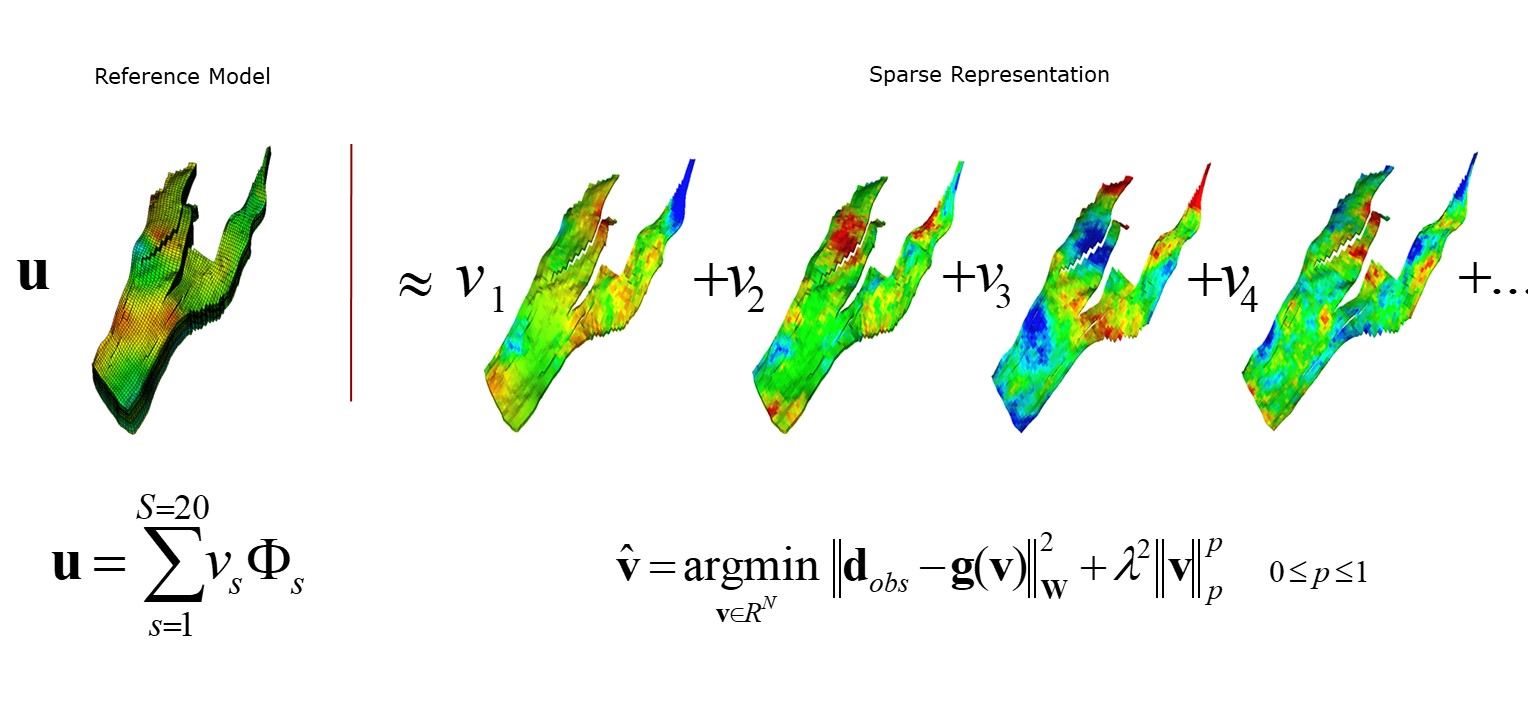
- Sparse representation for inverse modeling and dynamic data integration
- Inverse modeling under uncertain geologic scenarios
- Ensemble-based data assimilation
- Joint parameter estimation for coupled-physics models